基于fft算法的MATLAB仿真 - 可编程逻辑 -

该方法易于在FPGA上实现相关算法，比直接用相乘来得简单，而且但相关点数越多计算量相对而言比直接求解减少

仿真程序如下：

%步骤：

%（1） x，y都在高位补M（数据长度）个零

%（2） 求2M点FFT，X（K），Y（K）

%（3） 求乘积，Rxy（K）=X（K）*Y‘（K） 注：Y（K）取共轭

%（4） 求2M点IFFT， rxy= IFFT（Rxy（K））

clc;close all;clear all;

x1=load（‘D:My DocumentsMATLABdens_flow_ejieRF1.txt’）; %导入数据

y1=load（‘D:My DocumentsMATLABdens_flow_ejieRF2.txt’）; %导入数据

xcorr_size=512; %定义互相关的长度

xk=zeros（1，2*xcorr_size）;

yk=zeros（1，2*xcorr_size）;

label_x=zeros（1，2*xcorr_size）;

velo= zeros（1，2*xcorr_size）;

xk（1:xcorr_size）=x1（1:xcorr_size）; %以下为对比实验，将用fft相关算法和XCORR实现进行对比，发现不用使用反折方法也能实现相关

yk（1:xcorr_size）=y1（1:xcorr_size）; %实现效果非常好

XK_FFT=fft（xk）;

YK_FFT=conj（fft（yk））; %求共轭，只是在复数乘法之前加了一个 取共轭操作

ZK= XK_FFT.*YK_FFT;

rxy=fftshift（ifft（ZK））; %用取实部的操作一样

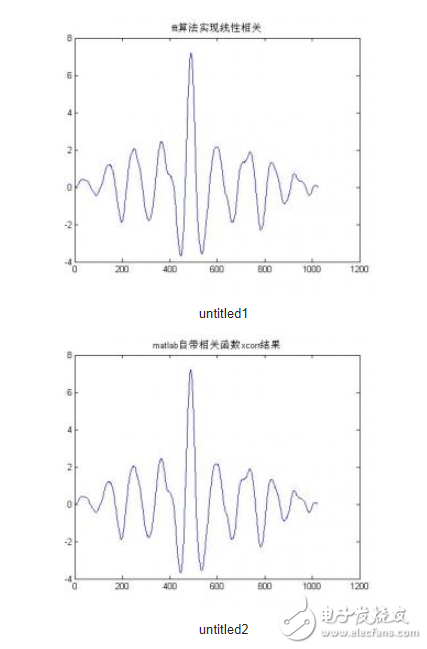
figure;

plot（rxy）;

TItle（‘fft算法实现线性相关’）;

rxy2=xcorr（xk（1:xcorr_size），yk（1:xcorr_size））;

figure;

plot（rxy2）;

TItle（‘matlab自带相关函数xcorr结果’）;

　　　　　　　　　　　　　 查看评论 回复