多普勒相位程序设计与实现 - FPGA/ASIC技术 -

摘　要：多普勒相位作为被测目标信息获取的重要来源，其计算精度成为基于FPGA实现合成孔径雷达实时回波模拟技术的关键要素。本文针对多普勒相位计算过程中存在的数值开方运算以及FPGA中专用开方器件的缺失性问题，在保证原始数据的仿真精度以及满足大位宽数据的仿真需求基础下，以Xilinx Virtex6 sx315t 为硬件平台，使用两种FPGA常用的近似方法——泰勒级数展开和CORDIC算法，对于多普勒相位的定点求解进行了程序设计与实现，并将仿真结果与MATLAB双精度理论数据进行对比，验证了精度的有效性。

 

１　引言

合成孔径雷达（SyntheTIc Aperture Radar ，简称SAR）作为一种高分辨微波成像雷达［１］，是地面信息获取的重要手段，它在国土测量、军事等领域发挥着重要作用。为确保所设计的SAR系统能够满足各个用户的具体需求，原始数据仿真和成像处理以及图像指标的评估已经成为SAR系统研制前的必需步骤。除此之外，在SAR实时成像系统研制以及地面处理的过程中，我们同样需要大量的模拟回波数据［２］。因此，SAR回波模拟技术能够为我们提供基本的研究手段和研究工具，它在SAR的发展和应用中，具有及其重要的作用。

作为雷达与目标相对运动的直观反映，多普勒相位是SAR回波模拟的原理依据，同样也是回波模拟精度的重要影响因素。在多普勒相位计算过程中存在数值开方运算，这使得其在FPGA（现场可编程门阵列）实现中存在两种主要限制因素：其一，FPGA硬件中不存在专门的开方器件；导致了开方运算在FPGA实现中的复杂性。其二，为了保证原始数据的仿真精度及适应大斜距数据的仿真，导致SAR回波模拟对FPGA定点运算中的斜距动态范围要求大［３］。

因此，本文针对SAR回波模拟中回波信号多普勒相位在FPGA实现中存在的限制，采用泰勒级数展开和CORDIC算法两种常用方法对其进行实现与仿真。

２　SAR回波模拟信号中的多普勒相位

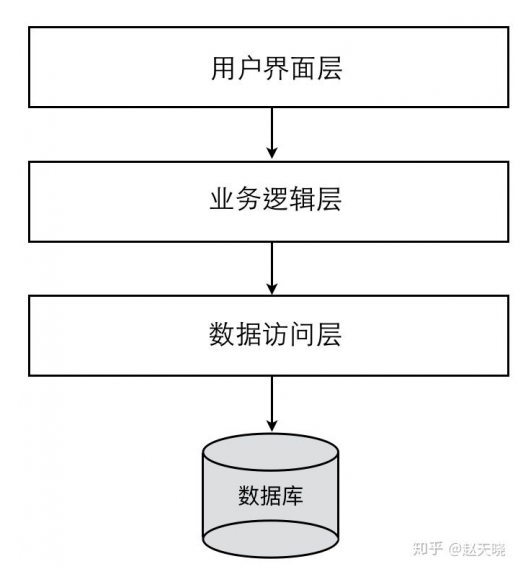
SAR的空间几何关系如图１，其中SAR飞行路径的地面航迹方向称为方位方向，与其垂直的方向称为距离方向［４］。

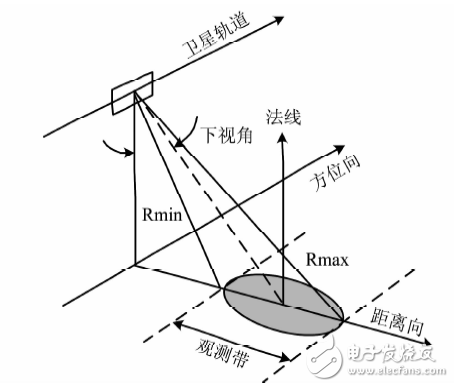
图１　SAR的空间几何关系

SAR在运动过程中，以特定的脉冲重复周期
（Pulse RepeTITIon TIme，简称PRT）发射并接收脉冲串，雷达天线波束照射到地面以后，照射区域内的各个点目标（又被称作散射元）对入射波进行后向散射。发射信号经过目标和天线方向图的调制，成为携带目标信息和环境信息的SAR回波。

SAR的发射脉冲串一般为线性调频（chirp）信号，设定SAR的发射脉冲串：

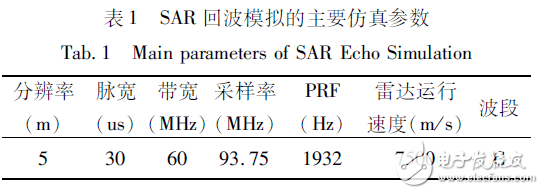
在本文中，要求斜距的近似误差最大为1/8波长，由表格１可见，目标点到SAR平台的斜距量级为106，动态范围很大；由于FPGA内部没有专用开方器件，使得多普勒相位运算过程复杂、速度低，在此使用泰勒级数展开与CORDIC算法。

３　基于泰勒级数展开的多普勒相位计算方法

泰勒级数是幂级数的一种，如果有了某一函数的幂级数展开式，则我们就可用它进行近似计算，即在展开式有效的区间范围上，我们可按照已知精确度要求，利用这个幂级数展开式将该函数值近似地计算出来。

　　　　　　　　　　　　　 查看评论 回复