数据挖掘: R, Python,Machine Learning,一起学起来!

大数据概念的火爆带动了相关工具方法的流行。大数据工具中，R和Python以其开源、免费、简单易用、大量算法库和社区支持等特质赢得了一众人心。机器学习则以其高大上的出身，和逐步广泛的应用，成为学习热点。越来越多的人有意学习这些工具、语言和算法。

想学就去学，还在等什么?让我们开始吧!

不同于典型的，先读书再做题，全部学会了再应用的学校真传学习法，我们来尝试另一种，带着任务学习，多头并进的方法。把R，Python和机器学习一网打尽。

线性回归，无疑是所有机器学习算法中最简单的一种，那么我们就从这里入手吧。想要了解线性回归原理和公式推导的，请自行搜索，网上的讲解、教案、课程堆积如山。我们今天要做的是，用R语言来验证线性回归模型。

说得更简单一点，我们自己先“伪造”一份数据，让它符合某种线性分布，然后用R语言对其进行训练，看训练得出的结果和我们的预设是否一致。

最简单的线性模型无外乎y = ax+ b。我们就用一份y = 1x + 2的数据来进行训练，看看R的计算结果能不能把a=1和b=2给找出来。

好了，下面大家一起跟我做:

1. 从https://cran.r-project.org/bin/windows/base/R-3.2.3-win.exe下载R for windows 3.2.3 (其实版本无所谓)

2. 安装R，然后打开R的GUI-RGui

3. 在RGui中运行如下这些命令:

1) > install.library("car")

# 安装“car”包，其中包括线性回归模型

2) > library(car)

#为下面调用car 库中的方法做准备

3) > x = c(1,2,3,4,5,6,7,8,9,10)

# 赋予x象限的数值

4) > y = c(3,4,5,6,7,8,9,10,11,12)

# 赋予y象限的数值

5) > plot(x,y)

# 对x和y的关系进行可视化展示，会看到下图

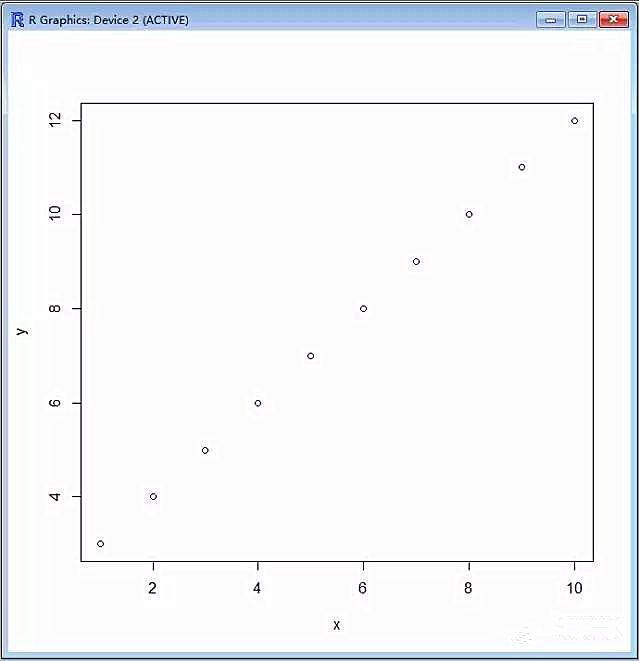
6) > lm.r=lm(y~x); lm.r

#将x和y的值带入linear regression model，(y ~ x)说明我希望得出一个y和x一次幂的映射，即我们要求的模型是一个从x到y的一元一次方程。换言之，我们要求两个值，a和b，这两个值使得(axi+ b - yi)^2的和达到最小。

输入这个命令后，你会看到如下显示:

Call:

lm(formula = y ~ x)

Coefficients:

(Intercept) x

2 1

这就意味着，训练出的模型结果为:y = 1x + 2，与我们的预期相符。

验证说明，说明R语言的线性回归库是有效的!

上面的例子有一点不方便的地方，数据需要手工输入，输入10个数字倒还罢了，要是成百上千的怎么办?其实很简单，我们可以把数据存储在文件中，R接受各种格式的文件输入。我们先看一下最简单的csv文件。

首先，我们得有一个csv文件。当然我们可以手工写一个。但是这样也挺累的，我们不如顺便学学Python，用Python生成一个吧。仍然跟我做:

1. 从https://www.python.org/ftp/python/3.4.4/python-3.4.4.msi下载一个Python for windows 3.4.4 (其实版本无所谓)

2. 安装Python ，然后打开它

3. 在Python.exe窗口中顺序输入如下命令

>>> from __future__import print_function

>>> f1 = open("./lrdata_1.csv","+w")

>>> f1.write("x,yn")

>>> for n in range(1,11):f1.write(str(n) + "," + str(n+2) + "n")

>>> f1.close()

于是我们就得到了lrdata_1.csv文件，内容如下:

x,y

1,3

2,4

3,5

4,6

5,7

6,8

7,9

8,10

9,11

于是，相应的R程序变成了如下这样:

> install.library("car")

> library(car)

> mydata = read.csv(".\lrdata_1.csv")

> x<-mydata[,1]

> y<-mydata[,2]

> x #看看x的内容

[1] 1 2 3 4 5 6 7 8 9 10

> y #看看y的内容

[1] 3 4 5 6 7 8 9 10 11 12

> lm.r=lm(y~x); lm.r

怎么样?是不是很容易?

我们再来试一个稍微复杂点的线性模型:y= 3x^2 + 4x + 7:

用Python生成数据文件:

>>> f1 = open(".\lrdata_2.csv","+w")

>>> for n in range(1,31):f1.write(str(n) + "," + str(3*n*n+4*n+7) + "n")

用R训练模型:

> mydata = read.csv(".\lrdata_2.csv")

> lm.r=lm(y~x+I(x^2)); lm.r

lm(formula = y ~ x + I(x^2))

(Intercept) x I(x^2)

7 4 3

注意:此处不再是lm(y~x)，而是lm(y~x + I(x^2))，说明我们要求取的模型是一个从x到y的一元二次方程

是不是超级简单?是不是觉得什么R, Python, MachineLearning, 不过就是如此而已?

责任编辑:王培