机器学习:Python实现多元线性回归
多元线性回归试图通过将线性方程拟合到观测数据来模拟两个或更多个解释变量与响应变量之间的关系。自变量x的每个值与因变量y的值相关联。
在最小二乘模型中,通过最小化从每个数据点到线的垂直偏差的平方和来计算观测数据的最佳拟合线(如果点恰好位于拟合线上,则其垂直偏差是0)。因为偏差是平方,然后求和,所以在正值和负值之间没有取消。最小二乘估计b0,b1,... bp通常由统计软件计算。
方差可以通过以下方式估算:
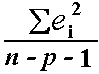
也称为均方误差(或MSE)。
标准误差s的估计是MSE的平方根。
所以这里我们处于SLR的相同情况,是对b和x的组合,这取决于我们考虑的变量的数量,我们有很多可以与我们的dipendent变量相关的回归变量。在我们构建LR模型之前快速了解线性回归:我们需要检查某些假设是否正确。因此,如果我们需要构建LR,我们必须确保验证这些假设:

当我们确定这些假设得到验证时,我们如何处理MLR中的虚拟变量?在这种情况下,虚拟变量将是状态/位置变量。正如我们为MLR所写的那样,我们首先编写公式:
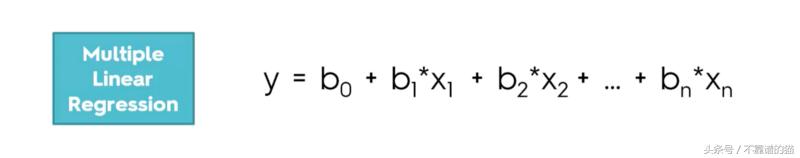
既然它不是一个数值,我们应该把状态放在这里?状态实际上是一个分类变量,因此我们不能将它添加到我们的等式中,我们需要对这种情况做一些事情,并且我们需要采用来处理分类变量的appraoch来创建虚拟变量。在这种情况下,我们有两个类别,我们需要创建一个新列并扩展我们的数据集。但是我们如何填充列?在这种情况下,我们将为纽约添加1,为加利福尼亚添加0,因此我们最终得到一个模型; 我们需要做的就是使用new york列并添加一个等于1的新变量D1(New York)和等于0的D1(California)。纽约列作为一个开关:如果它是1,我们知道是New York,如果它的0是California。因此,虚拟变量用作开关,并且不需要任何其他变量。当你研究这种方法时,它可能看起来有biased,因为对于加利福尼亚我们没有任何系数,但实际情况并非如此,因为LR工作的方式是它会考虑不包括在默认情况下的状态所以基本上加利福尼亚的系数是将在costant b0中被包含,并且默认情况下当D1等于0时,等式将变成加利福尼亚的等式。所以我们不能在我们的模型中同时包含这两个变量。如果我们这样做会怎么样?我们将一个变量复制为D2等于1 - D1并且会引发一个变量多线性问题,我们的模型无法正确识别我们的变量。这被称为虚拟陷阱,每次我们构机器学习建模型时,我们必须记住默认情况下始终考虑1个虚拟变量,因此如果我们有9个变量,我们应该只在公式中包含8个。

此外,我们如何优化我们的模型,因为我们有许多预测因子?我们需要决定我们要保留哪一个,因为如果我们考虑太多信息,我将成为垃圾模型。在模型优化中,我们可以实现5种主要方法:

All in方法是当我们知道每个回归量都有相关性或者我们只是必须使用这些变量时,或者我们是否准备Backward Elimination时。
Backward Elimination模型由下式给出:

Forward Selection模型有点复杂,因为我们必须构建一个模型并逐步添加具有层次值的新变量:

Bidirectional Elimination是Forward Selection和Backward Elimination模型的组合:

要在python中实现MLR,我们首先需要向模型添加更多变量,因此第一步是通过LABEL ENCODER类对我们的虚拟变量进行编码。为了避免虚拟变量陷阱,我们必须包括矩阵的所有列,除了默认情况下已经在我们的模型中编码的第一列:
# Data Preprocessing
# Importing the Library
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset= pd.read_csv('Data.csv')
X = dataset.iloc[: , :-1].values
Y = dataset.iloc[: , :4].values
# Encoding categorical data
# Encoding the indipendent variable
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X = LabelEncoder()
X[:, 3] = labelencoder_X.fit_transform(X[:, 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()
labelencoder_y = LabelEncoder()
y = labelencoder_y.fit_transform(y)
# Avoiding the Dummy Variable Trap
X = X[: , 1:]
# Splitting the dataset into the Training set and Test Set
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
下一步是通过LinearRegression类拟合或建模我们的数据集,就像我们对SLR所做的那样,并通过PREDICT方法预测测试集结果的预测向量y_pred,Python代码如下:
# Data Preprocessing
# Importing the Library
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset= pd.read_csv('Data.csv')
X = dataset.iloc[: , :-1].values
Y = dataset.iloc[: , :4].values
# Encoding categorical data
# Encoding the indipendent variable
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X = LabelEncoder()
X[:, 3] = labelencoder_X.fit_transform(X[:, 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()
labelencoder_y = LabelEncoder()
y = labelencoder_y.fit_transform(y)
# Avoiding the Dummy Variable Trap
X = X[: , 1:]
# Splitting the dataset into the Training set and Test Set
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
# Fitting Multiple Linear Regression to the Training set
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)
接下来,为了构建最优模型,我们首先实现了backward elimination方法,其中我们使用STATSMODELFORMULA库并包含X0(默认情况下库不考虑虚拟变量,因此我们必须通过APPEND和ONES函数添加一个新的向量n行和列,并通过astype(int)将数组转换为整数类型,Python代码如下:
# Data Preprocessing
# Importing the Library
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset= pd.read_csv('Data.csv')
X = dataset.iloc[: , :-1].values
Y = dataset.iloc[: , :4].values
# Encoding categorical data
# Encoding the indipendent variable
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X = LabelEncoder()
X[:, 3] = labelencoder_X.fit_transform(X[:, 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()
labelencoder_y = LabelEncoder()
y = labelencoder_y.fit_transform(y)
# Avoiding the Dummy Variable Trap
X = X[: , 1:]
# Splitting the dataset into the Training set and Test Set
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
# Fitting Multiple Linear Regression to the Training set
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)
# Predicting the Test set results
y_pred = regressor.predict(X_test)
# Building the optimal model using Backward Elimination
import statsmodel.formula.api as sm
X = np.append(arr = np.ones((50, 1)).astype(int), values = X, axis = 1)
backward elimination创建了一个称为X_opt的最佳特征矩阵,它是最具统计意义的特征,并将其初始化为包含所有变量的特征的原始矩阵,并创建一个名为regressor_OLS的新回归器fron sm库:
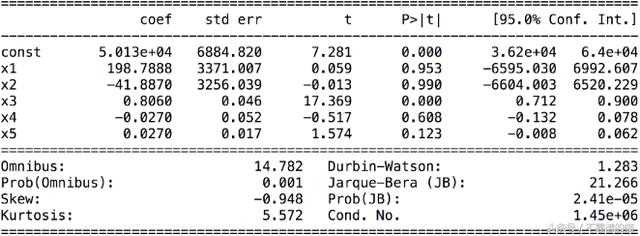
最后一步是通过函数可视化p值,并从最高p值开始消除对模型没有统计意义的变量。
# Data Preprocessing
# Importing the Library
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset= pd.read_csv('Data.csv')
X = dataset.iloc[: , :-1].values
Y = dataset.iloc[: , :4].values
# Encoding categorical data
# Encoding the indipendent variable
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X = LabelEncoder()
X[:, 3] = labelencoder_X.fit_transform(X[:, 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()
labelencoder_y = LabelEncoder()
y = labelencoder_y.fit_transform(y)
# Avoiding the Dummy Variable Trap
X = X[: , 1:]
# Splitting the dataset into the Training set and Test Set
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
# Fitting Multiple Linear Regression to the Training set
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)
# Predicting the Test set results
y_pred = regressor.predict(X_test)
# Building the optimal model using Backward Elimination
import statsmodel.formula.api as sm
X = np.append(arr = np.ones((50, 1)).astype(int), values = X, axis = 1)
X_opt = X[:, [0, 1 , 2 , 3, 4, 5]
refressor_OLS = sm.OLS(endog = y, exog = X_opt).fit()
regressor_OLS.summary()
X_opt = X[:, [0, 1 , 3, 4, 5]
refressor_OLS = sm.OLS(endog = y, exog = X_opt).fit()
regressor_OLS.summary()
X_opt = X[:, [0, 3, 4, 5]
refressor_OLS = sm.OLS(endog = y, exog = X_opt).fit()
regressor_OLS.summary()
X_opt = X[:, [0, 3, 5]
refressor_OLS = sm.OLS(endog = y, exog = X_opt).fit()
regressor_OLS.summary()
查看评论 回复

