RNN在FPGA的应用及测试分析 - FPGA/ASIC技术 -

循环神经网络（RNNs）具有保留记忆和学习数据序列的能力。由于RNN的循环性质，难以将其所有计算在传统硬件上实现并行化。当前CPU不具有大规模并行性，而由于RNN模型的顺序组件，GPU只能提供有限的并行性。针对这个问题，普渡大学的研究人员提出了一种LSTM在Zynq 7020 FPGA的硬件实现方案，该方案在FPGA中实现了2层128个隐藏单元的RNN，并且使用字符级语言模型进行了测试。该实现比嵌入在Zynq 7020 FPGA上的ARM Cortex-A9 CPU快了21倍。
 

LSTM是一种特殊的RNN，由于独特的设计结构，LSTM适合于处理和预测时间序列中间隔和延迟非常长的重要事件。标准的RNN可以保留和使用最近的过去信息，但是不能学习长期的依赖关系。并且由于存在梯度消失和爆炸的问题，传统的RNN无法训练较长的序列。为了解决上述问题，LSTM添加了记忆控制单元来决定何时记住、遗忘和输出。LSTM的单元结构如图1所示。其中⊙代表element-wise的乘法。

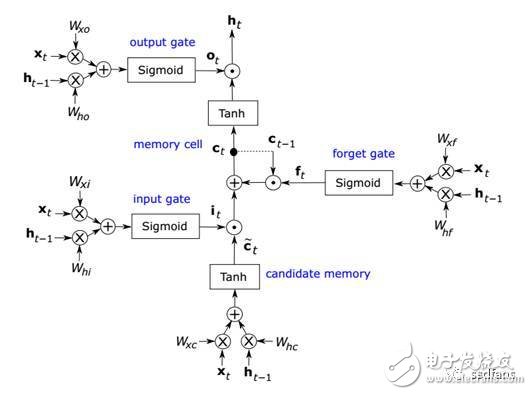
图1

用数学表达式表示图1如图2所示。其中表示Sigmoid函数，是层的输入向量，是模型参数，是记忆单元激活值，是候选记忆单元门，是层的输出向量。下标表示前一时刻，就是相应的输入、遗忘和输出门。这些门决定何时记住或遗忘一个输入序列，以及何时输出。人们需要对模型进行训练，从而得到所需的输出参数。简单来说，模型训练是一个迭代过程，其中训练数据被输入，然后将得到的输出与目标进行比较。模型通过BP算法进行训练。由于添加了更多的层和更多的不同的功能，模型可以变得相当复杂。 对于LSTM，每个模块有四个门和一些element-wise的操作。 深层LSTM网络具有多个LSTM模块级联，使得一层的输出是下一层的输入。

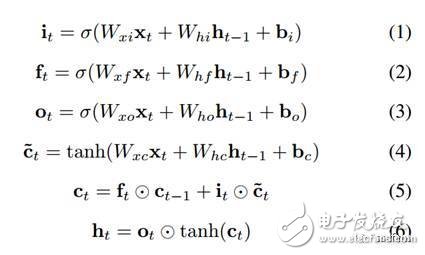
图2

了解完了LSTM的特性后，如何设计LSTM在FPGA上的实现呢？下面我们来看一下实现方案。

1）硬件

硬件实现的主要操作就是矩阵向量乘法和非线性函数。

矩阵向量乘法由MAC单元计算， MAC单元需要两个流：输入向量流和加权矩阵的行向量流。将相同的矢量流与每个权重矩阵行相乘并累加，以产生与权重矩阵的高相同尺寸的输出向量。在计算每个输出元素之后，MAC被重置以避免累积先前的矩阵行计算。可以通过向权重矩阵的最后一列添加偏置向量来将偏置b添加到乘法累加中，同时为输入向量增加一个额外的单位值。这样就不需要为偏置添加额外的输入端口，也可以向MAC单元添加额外的预配置步骤。 将MAC单元的结果加在一起。加法器的输出是一个元素的非线性函数，它是用线性映射来实现的。
非线性函数被分割成线性y = ax + b，其中x限于特定范围。在配置阶段，a，b和x范围的值存储在配置寄存器中。每个线性函数段用MAC单元和比较器实现。输入值与线性范围之间的比较决定是处理输入还是将其传递给下一个线性函数段模块。非线性函数分为13个线段，因此非线性模块包含13个流水线段模块。 实施设计的主要组成部分是如图3所示的门模块。

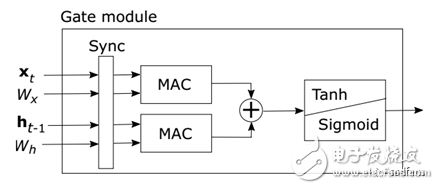
图3

实现模块使用直接存储访问（DMA）端口来进行数据的读入或写出。由于DMA端口是独立的，因此即使模块同时激活端口，输入流也不会同步。因此，需要流同步模块。该同步块用来缓存一些流数据，直到所有端口都是流式传输。当最后一个端口开始传输时，同步块开始输出同步流。这样就能确保到MAC单元的向量和矩阵行元素对齐。另外，图3中的门模块还包含一个将32位值转换为16位值的重分区块。MAC单元执行16位乘法，产生32位值。然后使用32位值执行加法以保持精度。

图2中的公式1,2,3,4都能用上述模块实现，剩下的只是计算公式5和6的一些element-wise的运算。为此，方案引入了如图4所示的包含额外的乘法器和加法器的模块。

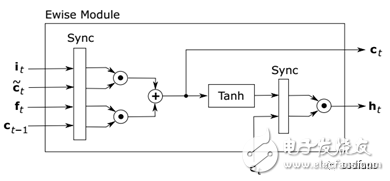
图4

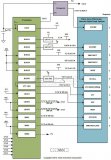
最终形成的实现LSTM的方案如图5所示。该方案使用图3中的三个模块和图4中的一个。门被预配置为具有非线性函数（tanh或S形）。内部模块由状态机控制以执行一系列操作。实现的设计使用四个32位DMA端口。由于操作以16位完成，每个DMA端口可以传输两个16位流。权重和连接在主存储器中以利用该特征。然后根据要执行的操作将流路由到不同的模块。

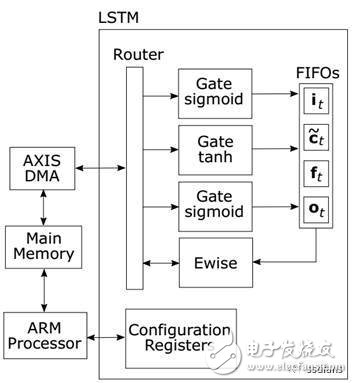
图5

2）驱动软件

　　　　　　　　　　　　　 查看评论 回复