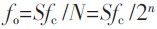对稀疏傅里叶变换并行算法研究并在FPGA上设计实现 - FPGA/ASIC技

摘要：提出了一种基于最优搜索的稀疏傅里叶变换(SFT)的并行实现设计。首先将输入信号分为并行N组，分别进行快速傅里叶变换(FFT)，实现信号频率分量的取模处理，然后通过排序搜索获得。经验证，相较于FFTW，当信号长度大于524 288时，执行时间会有更好的表现；相较于正交匹配算法及其他SFT的FPGA实现，其系统的复杂度降低了。
 

0引言

稀疏傅里叶变换（Sparse Fourier Transform, SFT）是一种新的算法框架，也是快速傅里叶变换（Fast Fourier Transform，FFT）在处理稀疏频谱信号上的延伸。2003年AYDINER A A等人提出了针对频域稀疏信号的傅里叶变换基本思想［1］。对于频域稀疏信号来说，其频谱可以通过其多级子集频谱获得。之后，IWEN M A等人从压缩感知得到启发，将采样和频率估计整合到快速傅里叶变换并提出了经典SFT框架［2］。之后SFT广泛运用于稀疏频谱信号（诸如音频信号、医学图像信号）的处理以及频谱感知领域［3］。大量的SFT算法被提出，它们多利用经典的频率估计算法通过亚奈奎斯特采样点的子集的傅立叶变换重构稀疏频点［4］。但由于经典SFT的亚奈奎斯特率样本是通过多次采样获得的，因此，经典SFT 不可能代替 FFT来处理实时信号，比如雷达信号等。

2010年以来，一种并行结构的SFT算法受到了广泛的关注［5］。并行SFT首先通过并行下采样，采集计算所需的所有时域数据，然后再通过FFT，通过亚线性频谱估计方法获得信号的稀疏频率及其幅值。由于该类方法以并行取代迭代获得频谱估计所需的所有信息，因此可以实时处理各种频域稀疏信号，使得经典SFT得到了改善。基于此，参考文献［6］~［8］探讨了稀疏傅里叶变换在GPU以及多核CPU上的实现方式。这些研究显示，基于GPU加速的实现方案运行速度要显著高于基于CPU的实现方案。然而，基于GPU的实现方案都存在主存储区与GPU存储区的连接交互问题，因此数据间的正常流动不能得到更好的促进。

为解决GPU的数据并行处理的局限性，本文研究SFT的并行算法并在FPGA上对其进行实现，同时应用中国余数定理（CRT）的基本原理对信号进行重构。相较于传统的SFT，本文的方法可以极大地降低系统的复杂度，减少了硬件的开销。本文，首先介绍SFT的并行框架，然后讨论SFT的FPGA实现架构，最后从仿真结果以及硬件实现两方面对系统进行评估。

1SFT并行算法

SFT并行算法主要由下采样、频率估计、幅度估计三个部分组成。在下采样过程中，将输信号划分为N个组，每个组的采样因子分别为σ1,σ2,…,σN。利用中国余数定理（Chinese Residue Theorem，CRT）进行频率以及幅度的估计，设定各组的采样因子两两互质。

并行SFT算法从L个采样样点中重构2 K算个参数，其中包括K个时延参数以及K个幅度参数。重构法的具体计算步骤如下：首先，设采样通道数为N，每个通道的采样点数分别为qi,i=1,2,…,N。计算X~=M*X，其中M为下采样矩阵，X为采样样本。之后，对X~进行DFT变换，得到X^=DFT(X~)。按幅度从大到小对X^向量中的值进行排序，计算hk：

hk=kthMAX|X^j|,k∈［0，K］（1）

其中K为指定的重构信号的参数。得到hk之后则可通过求余运算获取余数信息r1,khk的位置modq1。通过并行查询的方式搜索余数的最优解：

tminmint∈［0，qj］|hk-X^t*q1+r1,k|,j∈［2，N］（2）

rj,k=r1,k+tmin*q1modqj,j∈［2，N］（3）

利用CRT通过r1,b,…，rN，b重构时延参数τk，幅度估计参数可由公式（4）和 （5）得出：

x=real(hk)|τk

y=imag(hk)|τk(4)

ak=|x+iy|（5）

2SFT主要部分的FPGA实现

本文考虑使用MATLAB Simulink工具构建SFT采样算法的FPGA实现架构。图1展示了当采样通道数N=3时的SFT并行结构，其主要包括下采样、频率估计、幅度估计三个部分。　

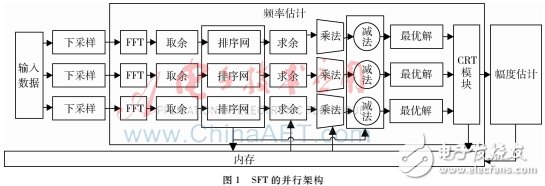
如图1所示，频率估计与幅度估计共用部分相同的硬件结构，信号在经过下采样之后，通过FFT运算得到复数的输出信号，为了对该复数信号进行排序，将该复数信号取模后送入排序网络，由于每个通道送入排序网络的点数不同，排序网络的结构会稍有差异。在利用CRT估计信号的幅度和频率之前，需要对信号进行求余、求最优解等运算。其中，最优解运算的核心是排序网络，利用排序网络的思想求取输入信号的最大值以及获取排序后的信号在原输入信号中的位置；CRT模块由一些加法器和乘法器组成。

　　　　　　　　　　　　　 查看评论 回复